To evaluate voltage unbalance we can use Symmetrical components method proposed by Charles Fortescue. Vector of three phase voltages can be expressed as a sum of three vectors (phasors): zero- positive- and negative-sequence.

\[ U_{abc} = \begin{bmatrix} U_a \ U_b \ U_c \end{bmatrix} = \begin{bmatrix} U_{a,0} \ U_{b,0} \ U_{c,0} \end{bmatrix} + \begin{bmatrix} U_{a,1} \ U_{b,1} \ U_{c,1} \end{bmatrix} + \begin{bmatrix} U_{a,2} \ U_{b,2} \ U_{c,2} \end{bmatrix} \] \[ \alpha \equiv e^{\frac{2}{3}\pi i} \] \[ \begin{align} U_{abc} &= \begin{bmatrix} U_0 \ U_0 \ U_0 \end{bmatrix} + \begin{bmatrix} U_1 \ \alpha^2 U_1 \ \alpha U_1 \end{bmatrix} + \begin{bmatrix} U_2 \ \alpha U_2 \ \alpha^2 U_2 \end{bmatrix} = \ \end{align} \] \[ \begin{align} &= \textbf{A} U_{012} \end{align} \]

From these phasors we can derive negative-sequence voltage unbalance ratio K2U and zero-sequence voltage unbalance ratio K0U

\[ K_{2U} = \frac{U_2}{U_1} \] \[ K_{0U} = \frac{U_0}{U_1} \]

Here is MATLAB script that produces the desired level of both negative- and -zero voltage unbalance ratio, then sets respective phasor magnitudes. After that we estimate unbalance using Symmetrical components method and draw a phasor diagramm.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

clear all; clc;
% K2U and K0U calculator
% in three phase system we accept that UB lags UA, and UC leads UA
% in balanced three phase system all angles are 120 deg=2*pi/3 rad
% color coding: UA=red UB=green UC=blue
K2U_ref=0.05; % set K2U = 5%
% magnitudes of the three phase voltages (rms)
mag_UA=100;
mag_UB=mag_UA*(1+2*K2U_ref)/(1-K2U_ref); % set magnitude so that K2U=K0U=K2U_ref
mag_UC=100;
% angles of voltages
phi_A  = degtorad(0);    % absolute angle of UA phasor
phi_AB = degtorad(-120);  % relative angle between UA phasor and UB phasor
                         % = phi_B-phiA 
phi_AC = degtorad(120);   % relative angle between UA phasor and UC phasor
                         % = phi_C-phiA

UA=mag_UA * exp(1i*(phi_A));
UB=mag_UB * exp(1i*(phi_A+phi_AB));
UC=mag_UC * exp(1i*(phi_A+phi_AC));

% calculate symmetrical components
a=exp(1i*2*pi/3); % complex angle constant
a2=a^2;
PSP = 1/3* (1*UA  + a *UB  + a2*UC); % Positive sequence phasor
NSP = 1/3* (1*UA  + a2*UB  + a *UC); % Negative sequence phasor
ZSP = 1/3* (1*UA  + 1 *UB  + 1 *UC); % Zero sequence phasor
% calculate K2U and K0U based on symmetrical components
K2U=abs(NSP)/abs(PSP)*100 % negative sequence ratio
K0U=abs(ZSP)/abs(PSP)*100 % zero sequence ratio

ROTATE_UI=angle(UA); % draw phasors relative to UA
figure;
h=compass(UA*exp(-1i*ROTATE_UI),'r'); hold on;
set(h, 'LineWidth',2);
h=compass(UB*exp(-1i*ROTATE_UI),'g');
set(h, 'LineWidth',2);
h=compass(UC*exp(-1i*ROTATE_UI),'b');
set(h, 'LineWidth',2);
legend('UA','UB','UC');

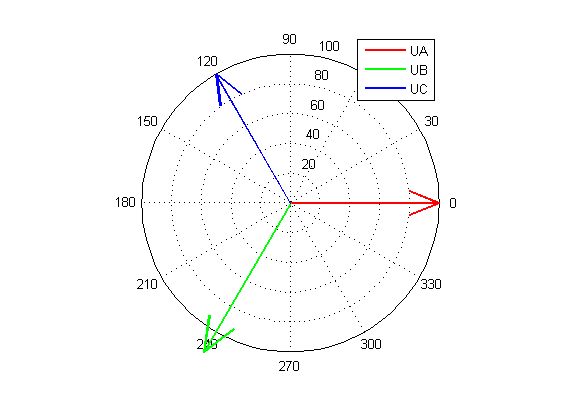
To generate signal with known level of unbalance $K_{2U}$ we can change magnitude of one of the voltages in the balanced three phase system. So we set all angles between voltages = 120 deg. Magnitudes of Ua and Uc should be equal (Ua=Uc). Ub should be set as

\[ U_b = U_a \frac{1+2 K_{2U} }{1-K_{2U}} \]

This equation can be easily derived if we notice that

\[ U_1 K_{2U} = \frac{1}{3} (U_b + 2 U_a) K_{2U} = \frac{1}{3} (U_b - U_a) = U_2 \]